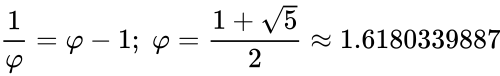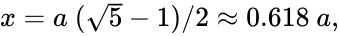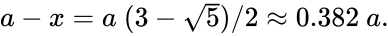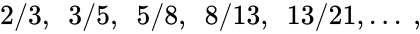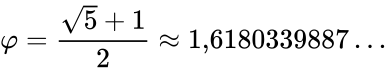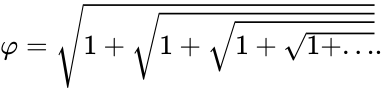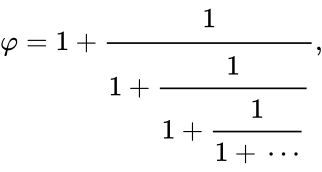Основы композиции. золотое сечение и пропорции фибоначчи в фотографии

Золотое соотношение во внутреннем оформлении

Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:

• Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
• Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
• При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
• При выборе цвета придерживайтесь примерно тех же правил:
• При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.

Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Пропорциональность — важная вещь

Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.

Суть универсальной пропорции

Принцип золотого сечения является всего лишь зависимостью чисел. Однако многие относятся к нему предвзято, приписывая этому явлению какие-то мистические силы. Причина кроется в необычных свойствах правила:

• Многие живые объекты обладают пропорциями туловища и конечностей, приближенными к показаниям золотого сечения.
• Зависимости 1,62 или 0,63 определяют отношения размеров лишь для живых существ. Объекты, относящиеся к неживой природе, очень редко соответствуют значению гармонического правила.
• Золотые пропорции строения туловища живых существ представляют собой неотъемлемое условие выживания многих биологических видов.

Золотое сечение можно найти в строении тел различных животных, стволов деревьев и корней кустарников. Сторонники универсальности этого принципа стараются доказать, что его значения жизненно важны для представителей живого мира.

Можно объяснить метод золотого сечения, используя образ куриного яйца. Отношение отрезков от точек скорлупы, в равной степени удаленных от центра тяжести, равно показателю золотого сечения. Самым важным для выживания птиц показателем яйца является именно его форма, а не прочность скорлупы.

Важно! Золотое сечение рассчитано на основе измерений множества живых объектов.

шкант березовый европартнер, 6х30мм, 50шт

Использование золотого сечения в искусстве

Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи. Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.

Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.

Ремонт или замена газового оборудования

Математические и эстетические свойства[править | править код]

(Рис.2) Построение золотого прямоугольника

Фигура (см. Рис.2) иллюстрирует геометрические отношения, которые определяют эту константу:

По крайней мере со времён Ренессанса, много художников и архитекторов строили свои работы так, чтобы приблизить золотое сечение (отношение) к правилам золотого прямоугольника, в котором отношение более длинной стороны к корткой было золотым отношением, равной золотой пропорции, удовлетворящее эстетические восприятия.

Алгебраически нахождение золотого сечения (см. Рис.2) отрезка длины сводится к решению уравнения:

, где = 1.6180339887 (для сравнения (см. Рис.1) ),

откуда:

Отношение может быть также выражено приближенно дробями

Иррациональное алгебраическое числоправить | править код

Отношение частей в этой пропорции выражается квадратичной иррациональностью

(Греческая буква «фи», первая буква имени Фидиас (Phidias), введённая для обозначения золотого сечения) — иррациональное алгебраическое число, положительное решение квадратного уравнения

представляется в виде бесконечной цепочки квадратных корней:

представляется в виде бесконечной цепной дроби

Золотое сечение в пятиконечной звезде

Построение золотого сечения

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 до н. э.), где оно применяется для построения правильного пятиугольника.

• В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны ).
• Геометрическое построение. Золотое сечение отрезка можно построить следующим образом: в точке восстанавливают перпендикуляр к , откладывают на нём отрезок , равный половине , на отрезке откладывают отрезок , равный , и наконец, на отрезке откладывают отрезок , равный . Тогда

Читайте еще больше на Яндекс Дзен

Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Тайна архитектуры Древней Греции

Красивые и гармоничные объекты всегда отвечают правилу ЗС, а при анализе величин определяется эта пропорциональность. Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?

Золотое сечение, что это такое. Понятие золотого сечения

Итак, золотое сечение – это золотая пропорция, которая также является гармоническим делением. Для того чтобы объяснить это более понятно, рассмотрим некоторые особенности формы. А именно: форма является чем-то целым, ну а целое, в свою очередь, всегда состоит из некоторых частей. Эти части, вероятнее всего, обладают разными характеристиками, по крайней мере разными размерами. Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.

Значит, другими словами, мы можем утверждать, что золотое сечение – это соотношение двух величин, которое имеет свою формулу. Использование такого соотношения при создании формы помогает сделать ее максимально красивой и гармоничной для человеческого глаза.

Золотое сечение в архитектуре

Множество построек древности, которые сохранились до сих пор, служат подтверждением тому, что архитекторы из эпохи средневековья были знакомы с гармоническим правилом. Очень хорошо заметно стремление соблюсти гармоническую пропорцию при сооружении церквей, значимых общественных зданий, резиденций королевских особ.

К примеру, собор Парижской Богоматери возведен таким образом, что многие из его участков соотносится с правилом золотого сечения. Можно найти немало произведений архитектуры 18 века, которые были построены в согласии с этим правилом. Правило применяли и многие русские архитекторы. Среди них был и М. Казаков, который создавал проекты усадеб и жилых зданий. Он проектировал здание сената и Голицынскую больницу.

Естественно, дома с таким отношением частей возводили и до открытия правила золотого сечения. Например, к таким зданиям относится церковь Покрова на Нерли. Красота здания приобретает еще большую загадочность, если учесть, что здание покровской церкви было возведено в XVIII веке. Однако современный вид постройка приобрела после реставрации.

В трудах о золотом сечении упоминается, что в архитектуре восприятие объектов зависит от того, кто наблюдает. Пропорции, образованные при помощи золотого сечения, дают максимально спокойное соотношение частей строения относительно друг друга.

Ярким представителем из ряда строений, соответствующих универсальному правилу, является памятник архитектуры Парфенон, возведенный еще в пятом веке до н. э. Парфенон устроен с восьмью колоннами по меньшим фасадам и с семнадцатью – по большим. Храм возведен из благородного мрамора. Благодаря этому использование раскраски ограничено. Высота строения относится к его длине 0,618. Если разделить Парфенон по пропорциям золотого сечения, получатся определенные выступы фасада.

Все эти сооружения имеют одно сходство – гармоничность сочетания форм и отменное качество строительства. Это объясняется использованием гармонического правила.

5 способов соблюдать правило в интерьере

1. В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.
2. Иногда достаточно переставить мебель или сделать дополнительную перегородку.
3. Аналогичным образом меняется высота и длина окон и дверей.
4. В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
5. Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.

Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.

Лавр Нобилис

Применение золотого сечения в кибернетике и технике

Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.

Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.

Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.

Цена за деталь

Золотая пропорция в строении легких человека

Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.

Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.

* Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.

Как исполнить заветное желание с помощью принципа золотого сечения

Принцип золотого сечения можно использовать и для исполнения желаний. Когда вы создадите формулу из слов по принципу золотого сечения, заложенная в этой формуле информация будет проходить прямо в подсознание, минуя ограничивающие убеждения и критику сознания.

Формулировать свои желания надо таким образом, чтобы полный текст состоял из 27 слов, а ключевое слово находилось в этой связке под номером 17. Если таких слов несколько (но не больше трех), так как одним словом часто невозможно точно выразить свое намерение, то можно занять позиции 16, 17, 18 (где под номером 17 должно идти основное слово).

Частицы, союзы и предлоги считаются за слова, это важно знать! Вы можете составить свой текст из 27 слов, 17-ое из которых будет ключевым, а можно просто воспользоваться вот таким шаблоном:

Это пример речевого «золотого сечения», где ключевое слово под номером 17 обращено напрямую к подсознанию.

Можно этот текст проговаривать, но для облегчения задачи лучше наговорить его на диктофон, настроить на режим повторения и прослушивать эту аудиозапись в течение 30-45 минут ежедневно. В это время можно заниматься своими делами, текст можно слушать как в наушниках, так и просто фоном, главное чтобы аудиозапись была вам слышна. Слушать эту запись надо в течение 15-ти дней.

Это интересно: «Энергетическая настройка на денежный поток»

Золотое сечение и гармония в искусстве[править | править код]

Золотое сечение и зрительные центры

Золотое сечение в видоискателях фотокиноаппаратры

Другим примером использования правила «золотого сечения» в киноискусстве служит расположение основных компонентов кадра в особых точках — «зрительных центрах». Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.

• Евклид (325–265 BC) в своих дал первое письменное определение золотого сечения, которое в переводе было названо «деление в крайнем и среднем отношении (extreme and mean ratio)» (греч. ακροςκαιμεσοςλογος).
• Фра Лука Пачоли (Fra Luca Pacioli) (1445–1517) совместно с Леонардо определил золотое сечение как «божественную пропорцию» в их труде «Божественная пропорция (Divina Proportione)».
• Леонардо да Винчи (1451–1519) совместно с Пачоли определил золотое сечение как «божественную пропорцию» в их труде «Божественная пропорция (Divina Proportione)» и, по-видиому, ввел термин золотое сечение (лат. gold aurea); см. Vitruvian Man.
• Иоганн Кеплер (Johannes Kepler) (1571–1630) называет золотое сечение «драгоценным камнем»: «Геометрия обладает двумя великими сокровищами: теорема Пифагора и деление отрезка в крайнем и среднем отношении; первое можно сравнить с мерой золота, второе назвать драгоценным камнем».

Как снять показания счетчика

Газовый счетчик предназначен для учета кубов израсходованного ресурса. Он также помогает значительно сэкономить на платежах за коммунальные услуги. Цена газа, если в помещении установлен счетчик, значительно ниже, чем там, где его нет. Благодаря этому устройству оплата рассчитывается только за израсходованный ресурс, а не за его среднее количество. Потребитель может сам планировать свои расходы, учитывая данные прибора. Передача показаний за газ упрощает расчет оплаты. Потребителю сообщают сумму, которую следует оплатить.

https://youtube.com/watch?v=mCFVfZJOKy0

Чтобы снять показания, следует стать напротив счетчика. Смотреть необходимо прямо на циферблат. Любой счетчик, независимо от модели, имеет отсчетный механизм. Он может быть восьми-, семи- и пятиразрядным. Целые кубометры разделены запятой. Далее идут 10-е, 100-е и 1000-е, которые разделяют разными цветами.

Пять данных вправо до запятой — это и есть те цифры, которые указывают на использованные кубометры газа. Их следует отнять от тех, которые были переданы и оплачены в предыдущем месяце. Теперь можно передать показания за газ. Нижегородэнергогазрасчет (так называется Нижегородский расчетный отдел) — эта или другая компания — требования практически везде одинаковы. Хотя каждая область может вносить небольшие нюансы в возможности и числа передачи, даже цена может несколько варьировать.

Пример расчета

Так как передать показания счетчика за газ? Нижегородэнергогазрасчет, Самарагаз, Комирегионгаз, ООО Смолрегионгаз или Регионгаз34 — все абсолютно компании принимают фактические показатели израсходованного газа. Чтобы правильно подать эти данные, внимательно смотрим на счетчик. На циферблате — 00364,016. Записываем пять номеров до запятой вправо. На данные после запятой не обращаем внимания (они часто находятся на поле иного оттенка). В квитанцию вписываем 364. Это число передаем в газовую компанию.

Обычно показания принимаются с первого по пятое число каждого месяца. Если клиент не передает своевременно показания, объем израсходованного ресурса начисляется методом расчета.

Потребитель каждый месяц оплачивает количество потребленных кубов полезного ископаемого. Сумма оплаты за него. Чтобы с точностью рассчитать количество потребленного по счетчику газа, следует:

• запомнить или отметить показатели с первого месяца одного месяца по первое число следующего;
• передать эти данные в компанию, занимающуюся газоснабжением.

Математическое выражение золотой пропорции

Математика дает очень четкое определение пропорции, которое говорит о том, что она является равенством двух соотношений. Математически это можно выразить таким равенством: а:b=с:d, где а, b, с, d – это некоторые определенные значения.

Если рассматривать пропорцию отрезка, разделенного на две части, то можем встретить всего несколько ситуаций:

• Отрезок разделен на две абсолютно ровные части, а значит, АВ:АС= АВ:ВС, если АВ – это точна начала и конца отрезка, а С – точка, которая и разделяет отрезок на две равные части.
• Отрезок разделен на две неравные части, которые могут находиться в самом разном соотношении между собой, а значит, здесь они абсолютно непропорциональны.
• Отрезок разделен так, что АВ:АС= АС:ВС.

Что же касается золотого сечения, то это такое пропорциональное деление отрезка на неравные между собой части, когда весь отрезок относится к большей части, как и сама большая часть относится к меньшей. Существует и другая формулировка: меньший отрезок так относится к большему, как и больший ко всему отрезку. В математическом соотношении это выглядит следующим образом: а:b = b:с или с:b = b:а. Именно такой вид имеет формула золотого сечения.

Подборка фото с примерами из интерьеров

Золотое сечение в природе

Золотое сечение и последовательность Фибоначчи имеет множество проявлений в природе, в частности в лепестках и семенах цветов. Если присмотреться к семенам подсолнуха, то можно увидеть что они растут по спирали, которая имеет сходство с золотой спиралью. 

Спирали Фибоначчи просматриваются во многих явлениях природы, примеры вы можете увидеть на картинке.

В природе существует очень много примеров золотого сечения, его можно увидеть в форме ракушек моллюсков, снежинок, кактусов, шишек и другихИсточник yandex.net

По такому же закону построены ураганы, паутина, молекула ДНК, яйцо и стрекоза.

Яйцо построено по принципу золотого сеченияИсточник homius.ru

Если вы взглянете на свои руки, то заметите, что соотношение фаланг пальцев, первой ко второй и к третьей, а также костей предплечья в сравнении с рукой, всегда равняется 1,618. То же самое с лицом и другими частями тела.

Мифы и диковинные факты о пирамиде

Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?

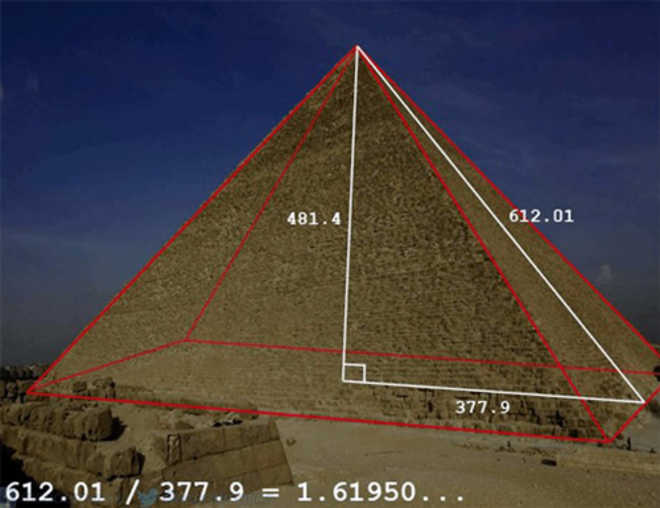
Но тогда возникает вопрос об уровне древнеегипетской математики. Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного

Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?

Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.

Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.

Золотая пропорция в математике

Первое знакомство с золотым сечением на практике начинается с простого деления отрезка прямой все в тех же пропорциях. Чаще всего это реализуется с помощью линейки, циркуля и, конечно же, карандаша.

Отрезки золотой пропорции выражают как бесконечную иррациональную дробь AE = 0,618…, если АВ принимается за единицу, ВЕ = 0,382… Для того чтобы сделать эти вычисления более практическими, очень часто используют не точные, а приближенные значения, а именно – 0,62 и 0,38. Если же отрезок АВ принимать за 100 частей, то большая его часть будет равна 62, ну а меньшая – 38 частям соответственно.

Главное свойство золотого соотношения можно выразить уравнением: х2-х-1=0. При решении мы получаем следующие корни: х_1,2=. Хотя математика и есть точной и строгой наукой, как и ее раздел – геометрия, но именно такие свойства, как закономерности золотого сечения, наводят таинственность на эту тему.

Золотое сечение — что это?

Одним из самых мощных композиционных правил в фотографии является правило золотого сечения, которое еще называют “божественной пропорцией”. Согласно ему, кадр необходимо разделить на девять частей — двумя линиями по горизонтали и двумя по вертикали. На пересечении линий образовываются четыре точки, называемые узлами внимания — это самые активные области на фотографии, на которые приходится больше всего внимания. Именно там и на самих линиях необходимо размещать главные объекты и расставлять акценты.

Композиция должна состоять из нескольких частей — таких, чтобы вся горизонталь отрезка имела в соотношении большую и меньшую части, одинаково пропорциональные к основной длине. Параметры золотого сечения составляют 1:0.618:1.

История возникновения правила

Свои истоки правило берет с древнейших времен: первые упоминания о нем найдены в трудах Евклида “Начала”, которые были написаны около 300 лет до н. э. Там он применял принцип деления отрезка в крайнем и среднем отношении для построения правильного пятиугольника, который тоже называют золотым.

По другой версии, за закон золотого сечения человечество должно быть благодарно Пифагору, который сам сделал это открытие и поведал о нем остальным. Но Пифагор был не только известным математиком, но и мистиком, поэтому открытие данного правило обросло мистическими значениями и потусторонними смыслами

Последователи великого мыслителя не брали во внимание такие домыслы, а лишь руководствовались этим правилом для создания прекрасных скульптур, сооружений и барельефов

Интересный факт: эти золотые пропорции использовались в жизни древних людей, а точнее — египтян. По правилам золотого сечения сконструированы пирамида Хеопса, египетский храм Парфенон, барельефы и даже украшения, которые найдены в гробнице Тутанхамона.

Поучаствовал в поиске идеальных пропорций и итальянский математик Леонардо Фибоначчи, которому удалось выявить удивительную закономерность. Случилось это примерно в 1200 году. Ученый тогда заметил, что в природе и окружающей нас действительности есть определенная схема, которой все подчиняется и которая очень приятна человеческому глазу. Он поставил в ряд определенные числа и заметил, что каждая часть последовательности является результатом сложения двух предыдущих. Благодаря этой последовательности мир увидел знаменитые спираль и сетку Фибоначчи, которые используют в построении грамотной композиции до сих пор.

Как выбрать систему умного дома

Математические свойства

• Φ{\displaystyle \Phi } — иррациональное алгебраическое число, положительное решение квадратного уравнения x2−x−1={\displaystyle x^{2}-x-1=0}, откуда, в частности, следуют соотношения:

  Φ2−Φ=1,{\displaystyle \Phi ^{2}-\Phi =1,}

  Φ⋅(Φ−1)=1.{\displaystyle \Phi \cdot (\Phi -1)=1.}

• Φ{\displaystyle \Phi } — представляется через тригонометрические функции:
  • Φ=2cos⁡π5=2cos⁡36∘.{\displaystyle \Phi =2\cos {\frac {\pi }{5}}=2\cos 36^{\circ }.}
  • Φ=2sin⁡(3π10)=2sin⁡54∘.{\displaystyle \Phi =2\sin(3\pi /10)=2\sin 54^{\circ }.}

1Φ=φ=tg⁡(arctg⁡(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

• Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:

  Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}

• Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби

  Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

• Φ=limn→∞Fn+1Fn.{\displaystyle \Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}.}

• Мера иррациональности Φ{\displaystyle \Phi } равна 2.

Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

Золотое сечение в пятиконечной звезде

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

Построение золотого сечения

Геометрическое построение. Золотое сечение отрезка AB{\displaystyle AB} можно построить следующим образом: в точке B{\displaystyle B} восстанавливают перпендикуляр к AB{\displaystyle AB}, откладывают на нём отрезок BC{\displaystyle BC}, равный половине AB{\displaystyle AB}, на отрезке AC{\displaystyle AC} откладывают отрезок CD{\displaystyle CD}, равный BC{\displaystyle BC}, и наконец, на отрезке AB{\displaystyle AB} откладывают отрезок AE{\displaystyle AE}, равный AD{\displaystyle AD}. Тогда

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }.

• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
• Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны.
• ∑n=1∞(−1)n+1n2(2nn)=2ln2⁡φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }

Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]